06 - RELAÇÕES E FUNÇÕES

RELAÇÕES E FUNÇÃO


CONCEITOS DE RELAÇÃO R DE A EM B


Considere os conjuntos;

A = { 1,2,5}
B = { 2,4}

Formemos o produto cartesiano de A por B:

A x B = { (1,2), (1,4), (2,2), (2,4), (5,2) , (5,4) }

Exemplos:

Sejam A = { 1,2,3} e  B = { 5,6}, os subconjuntos de A x B :

R1 = { (1,5),(2,6), ( 3,6)}

R2 = { (2,6), (3,5)}

R3= { (1,6) ,(2,6),(3,5),(3,6)}

são relações de A em B

EXERCÍCIOS

FUNÇÃO

Uma relação de A em B é determinada de função ou aplicação quando associa a todo elemento de A um único elemento em B

Exemplos

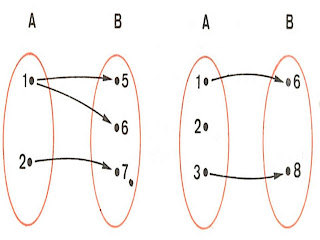
São funções de A em B, as relações representadas nos diagramas:

Obeserve:

-Em A, não sobra elementos, em B pode sobrar

- Em A, de cada elemento "parte"uma unica flecha

- Em B, um elemento pode receber mais de uma flecha

Não são funçoes de A em B, as representadas no diagramas:

Exercícios

1) Indique os diagramas que representam uma função de E em F:

DOMÍNIO CONTRADOMÍNIO E CONJUNTO IMAGEM DE UMA FUNÇÃO

Seja f uma função de A em B.

f = { (1,2),(2,4),(3,6)}

O conjunto A é o dominio da função (conjuntode partida)

No exemplo temos:

domínio = { 1,2,3}

O conjunto B é o contradominio da funbção (conjunto de chegada)

No exemplo, temos:

contradominio = { 2,3,4,5,6,7}

A imagem da função é formadapor todos os elementos de B que ficam associados a elemntos de A (elementos de B que rebem flechas )

No exemplo temos :

imagem = { 2,4,6}

O conjunto imagem é um subconjunto do contradomínio.

NOTAÇÃO DE FUNÇÃO

Considere a função f definida de R em R, tal que y = 2x + 1.

Observ e, por exemplo, que:

Para x=3, temos y = 2 . 3+1 = 7

para x=4, temos y = 2 . 4 +1= 9

para x = 5, temos y = 2 . 5 +1 = 11

Dizemos que:

7 é a imagem de 3 pela função f.  [Escreveos f(3) = 7]

9 é a imagem de 4 pela fução f  [escrevemos f(4) = 9]

11 é a imagem de 5 pela função f  [ escrevemos f(5) = 11]

Então:

Em vez de escrever y = 2x + 1, podemos escrever f(x) = 2x + 1

Onde:

x --- reprsenta um elelmento genérico do domínio da função

f(x) ---- representa o valor da função para o x considerado.

Nota:

Para definir uma função, é necessário especificar o seu domínio e o seu contra-dominio. Neste livro estudaremos as funções definidas de R em R

EXERCÍCIOS RESOLVIDOS

1) Dada a função definida por:

2) Dada a função definida por:

EXERCÍCIOS

EXERCÍCIOS COMPLEMENTARES

1) Entre as relações abaixo dadas por diagrama, quais são as funções de G em H

xxxxxxxxxxxxxxxxxxxxxxx