8° SÉRIE - 9º ANO: outubro 2011

RELAÇÃO MÉTRICAS NA CIRCUNFERENCIA

TEOREMA

Se duas cordas se cortam em um ponto interior da circunferecia, então o produto das medidas dos segmentos determinados numa delas é igual ao produto das medidas dos segmentos determinados na outra

Demonstração:

Considerando o triângulo PAD e PCB

EXERCÍCIOS RESOLVIDOS

Calcule o valor de x na figura:

EXERCICIOS

1) Calcule o valor de x nas seguintes figuras:

(R:12)

(R: x= 9)

(R: x = 6)

(R: x= 9)

(R: x = 4)

TEOREMA

Se de um ponto p que pertence ao exterior de um circunferencia traçamos duas secantes que cortam a circunferência,respectivamente nos pontos A,B e C,D

PA . PB = PC . PD

Demonstração

Considerando os triângulos PAD e PCB

EXERCÍCIOS RESOLVIDOS

Calcular o valor de x na figura:

EXERCÍCIOS

1) Calcule o valor de x nas seguintes figuras:

R: x = 14

R: x = 4,5

R: x = 4

R: x = √32

R: x = 14

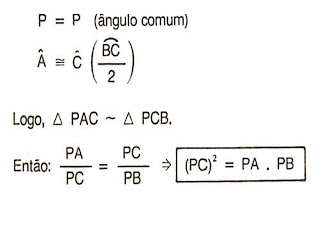
TEOREMA

Se de um ponto P que pertence ao exterior de uma circunferencia, traçamos uma tangente e uma secante que encontram a circunferencia respctivamente, nos pontos C e A e B , então:

(PC)² = PA . PB

Demonstração:

Considerendo os triângulos PAC e PCB:

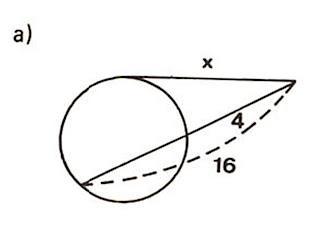
Exercícios Resolvido

Calcular o valor de x na figura:

EXERCÍCIOS

1) Calcule o valor de x nas seguintes figuras:

R: x = 8

R: x = 6

R: x²= 2

R: x = 7,5

POLÍGNOS RELUGARES

POLÍGNO INSCRITO NUMA CIRCUNFERÊNCIA

Dizemos que um polígno é inscrito quando todos os seus vértices pertencem à circunferência.

veja:

A circunferência está circunscrita ao poligono.

POLÍGONO CIRCUNSCRITO A UMA CIRCUNFERÊNCIA

Dizemos que um poligno é circunscrito quando todos os seus lados são tangentes à circunferência

Veja:

A circunferência está inscrita no polígno.

POLÍGONO REGULAR

Um poligono é regular quanto têm os lados congruentes e os ângulos congruentes

veja:

Os poligonos regulares podem ser inscritos ou circunscritos a uma circunferência

APÓTEMA DE UM POLIGONO REGULAR

Apótema é o segmento cujas as extremeidades são o centro e o ponto médio do lado.

RELAÇÕES MÉTRICAS NOS POLÍGONOS REGULARES

1) QUADRADO

EXERCÍCIOS RESOLVIDOS

Calcular a medida do lado e do apótema do quadrado inscrito numa circunferência de raio 8 cm

solução:

EXERCICIOS

1) Calcule o lado de um quadrado inscito numa circunferência de raio 6m

R: 6√2 cm

2) Calcule o lado de um quadrado inscrito numa circunferência de raio 5√2 cm .

R: 10 cm

3) Calcule o apótema de um quadrado inscrito numa circunferência de 5√8 cm

R: 10 cm

4) O lado de um quadrado inscrito numa circunferência mede 10√2 cm . Calcule o raio da circunferência

5) Calcule o lado e o apótema de um quadrado inscrito numa circunferência de raio 12√2 cm

R: 12 cm

6) A medida do apótema de um quadrado inscrito numa circunferencia é 15 cm calcule o raio da circunferencia ,

R: 15√2 cm

R: 10 cm

RELAÇÕES MÉTRICAS NUM TRIÂNGULO QUALQUER

TEOREMA - LADO OPOSTO A ÂNGULO AGUDO

Quando da ,medida do lado oposto a um ângulo é igual à soma dos quadrados das medidas dos outros dois lados, menos duas vezes o produto da medida de um desses lados pela medida da projeção do outro sobre ele.

EXERCÍCIOS

TEOREMA - LADO OPOSTO A ÂNGULO OBTUSO

O quadrado da medida do lado oposto ao ângulo é igual à soma dos quadrados das medidas dos outros dois lados, mais duas ve\zes o produto da medida de um desses lados pela medida da projeção do outro sobre ele.